電気回路で,回路の各部の電圧や電流の値を求めようとすると,それらを変数とした連立方程式を立て,その解を求める計算を行わねばならなくなる。また,電気回路に限らず,連立方程式は,これからの専門科目の学習を通じてさまざまなところで登場する。物理法則に基づく連立方程式の立て方については,これからの専門科目の学習を通じて習得することとして,ここでは,その解を確実に求めることができるよう,その解法から学習を始めることとしよう。

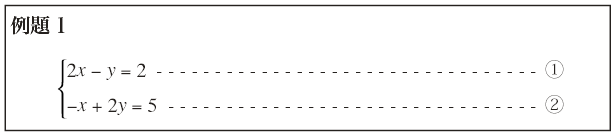
上のような,複数個の未知数を含み,かつすべての方程式が未知数についての1次方程式からなっているような方程式を連立1次方程式という。未知数の個数が2個,3個により,2元連立1次方程式,3元連立1次方程式という。例題1は,x, yを未知数とする2元連立1次方程式である。
連立1次方程式を解くとは,与えられた方程式をすべて同時に満足する未知数の値を求めることである。そのためには,代入法や加減法あるいは等置法などといった解法があり,それらを用いて順に未知数を消去していき,最終的に1元方程式として解を導く。

代入法と加減法は混在して使ってよい。例題1の〈加減法による解法〉において,y = 4が求まった段階で,2 ×![]() +
+![]() を作ってxを求めなくとも,y = 4を
を作ってxを求めなくとも,y = 4を![]() または
または![]() に代入してx = 3を求めてもよい。
に代入してx = 3を求めてもよい。
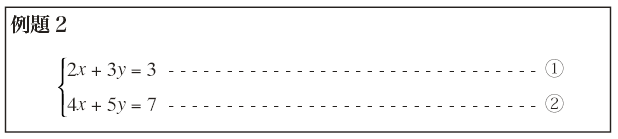

例題2の2つの解法を比べてみると,代入法だけより加減法と代入法を使うことにより,計算がはるかに楽になっている。従って,計算ミスも減少する。連立方程式の解法を確実なものとするには,多くの問題を解き,代入法と加減法をうまく使って,より楽に早く解ける方法を会得することである。
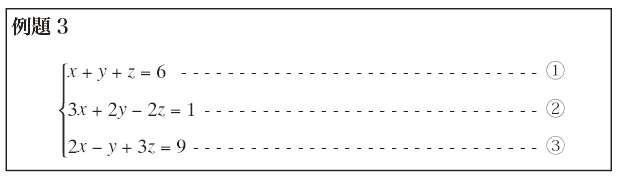
3元連立1次方程式は,どれか1つの未知数を消去して2元連立1次方程式を導き,それを例題1, 2のように解く。

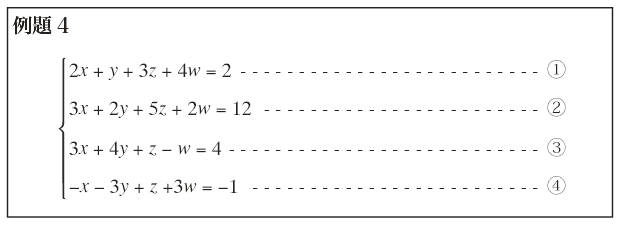
以上の説明で既に推測がつくと思うが,4元連立1次方程式を解くには,1つの未知数を消去して3元連立1次方程式を導き,それから更に残りの1つの未知数を消去して2元連立1次方程式を導き,それを解けばよい。一般のn元連立1次方程式についてもこの操作を続けて行えばよいのだが,未知数が多いときには,この操作は結構面倒である。このようなときは,線形代数の講義で学ぶ「掃き出し法」で解けばよい。

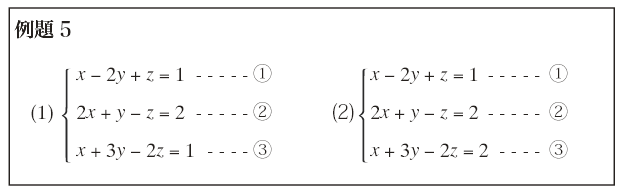

例題5のように,連立1次方程式は常にすっきりと唯一つの解を持つとは限らない。このような場合の扱いについては,線形代数の講義で学ぶこととし,ここではすっきりと唯一つの解を持つ場合に,その解を求める計算力を養うことを目標とする。
解説:図の回路はキルヒホッフの法則を適用して解く問題の典型的な例題で,電源の向きや抵抗の配置によってさまざまな変形が考えられるが,大事な問題である。
キルヒホッフの法則電気回路における電圧と電流の関係を表す法則で, 電流則:1点に流入する電流は流出する電流に等しい。 電圧則:1周する回路において向きを考慮して加えた電圧は0となる。 の2つがある。電流則は「水の流れのようなものであり,入ったものは出てゆく」ということであり,電圧則は「電気にも高さに相当するものがあり,山登りで登山口に戻れば結局上った高さは0となる」ということに対応している。 |
キルヒホッフの法則を適用して電圧・電流の関係式を求める方法は電気回路で学ぶ。ここでは,その得られた結果が連立1次方程式になることを認めて,流れる電流を求めてみよう。
