1.2 連立１次方程式(2)

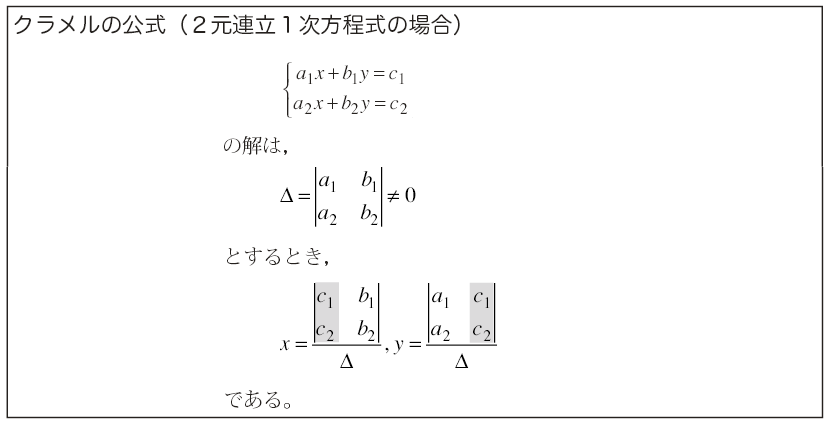
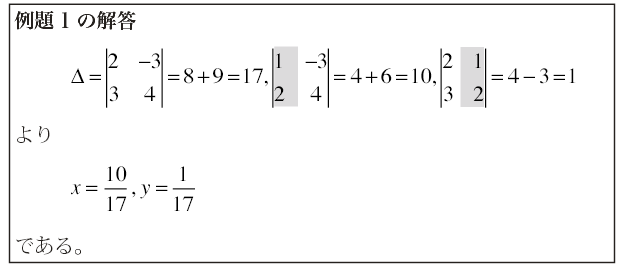
　この節では，連立1次方程式の解についての「クラメルの公式」を学ぶ。ただし，証明等については線形代数の講義で行うこととし，ここでは計算のやり方のみを説明する。

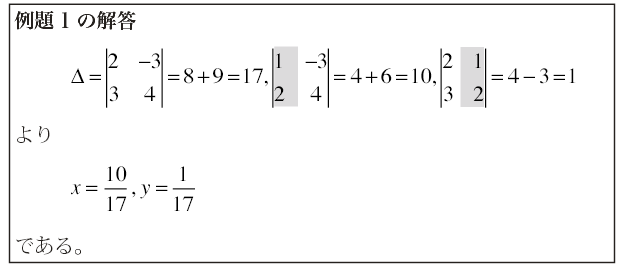
　クラメルの公式は，一般のn元連立1次方程式に対しても成立しているが，ここでは3元連立1次方程式までを示すこととする。

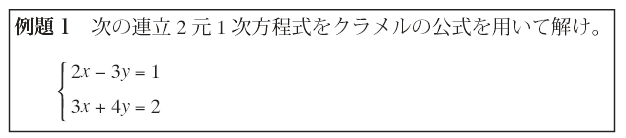
　連立1次方程式を解く場合，係数が数値ばかりであるならば，1.1節で学んだ代入法や加減法で十分解けるが，係数に文字が含まれる場合には計算が非常に煩雑になる。この場合，上で述べたクラメルの公式が威力を発揮する。たとえば，1.1節の例題６をクラメルの公式を用いて解いてみよう。

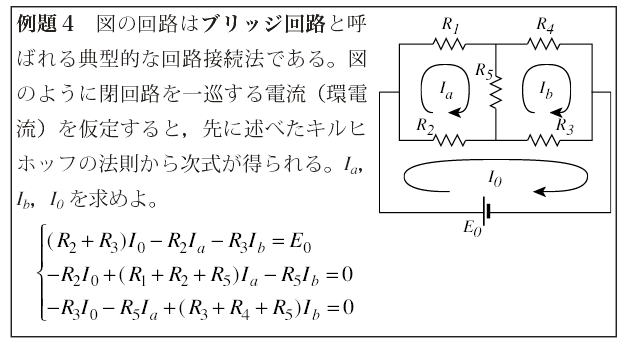
解説：電気回路では1.1節の例題6で与えたように，回路の枝を流れるものとして電流を扱う（枝電流）こともできるし，ここで与えたように，閉回路を一巡するものとして電流を扱う（環電流）こともできる。枝電流と環電流は，たとえばこの例題のブリッジ回路においてR5を下向きに流れる電流I5は(Ia - Ib)に等しくなるとの関係にある。

　例題4の解答においてを行列式の定義通りにδを求めると，

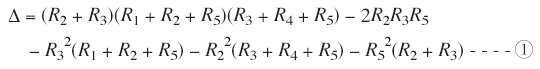
となる。これを展開してまとめると，解答に示しているδ，すなわち，

となる。この計算は少々面倒である。しかし行列式の性質を使ってδを求めると，この面倒な計算を行うことなく直接が求められる。このようなことは線形代数の講義で解説される。