(4) -5π/4 (5) 7π (6) 12π/35
問2 半径がr,中心角がθである扇形の弧の長さと面積を求めよ。
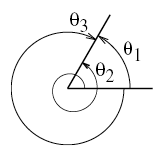 角を図形的なものとして考える時には角は0から2πまでの値で十分であるが,角を回転量を表すものとして考える時には,何周回転しているか,また時計回りに回転しているのか反時計まわりに回転しているのかといったことによって,2πより大きい角や負の角も考える必要が生じる。その場合,左図のような角が与えられても,その大きさはθ1ともθ2ともθ3ともあるいはその他の角とも考えられ,その表し方に工夫が必要である。ところで,これらの角の値の差はすべて2π(1回転)の整数倍になるので,次のように表すことにより,すべての場合を示すことができる。
角を図形的なものとして考える時には角は0から2πまでの値で十分であるが,角を回転量を表すものとして考える時には,何周回転しているか,また時計回りに回転しているのか反時計まわりに回転しているのかといったことによって,2πより大きい角や負の角も考える必要が生じる。その場合,左図のような角が与えられても,その大きさはθ1ともθ2ともθ3ともあるいはその他の角とも考えられ,その表し方に工夫が必要である。ところで,これらの角の値の差はすべて2π(1回転)の整数倍になるので,次のように表すことにより,すべての場合を示すことができる。
このように表した角を一般角という。具体的な問題において角を一般角で表すか,それともその中の1つの角で表せばよいかは,そのときの状況により判断して決定する。
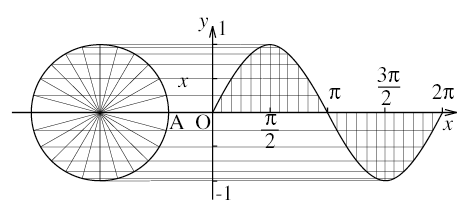
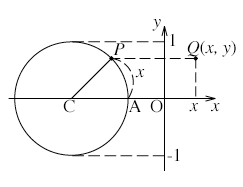 それではここで,角をラジアンで表した場合の三角関数y = sinx のグラフを描いてみよう。図のようにx軸上に中心をもつ半径1の円を描き,この円周上に点Pをとる。∠ACPの大きさ(符号つきのAPの長さx)を始点Aから測ると,sinxの値は点Pからx軸へ下ろした垂線の長さ(= 点Pのy座標)となる。それをxの関数としてグラフに描くために,点Pをx軸に並行に移動して,原点Oからxの距離まで移動した点をQとし,点Pが円周上を1周以上移動した場合や反時計まわりに移動した場合も含めてすべての場合について,点Qの描く軌跡を記録する。すると,この点Qの描く軌跡がy = sinxのグラフとなる。
それではここで,角をラジアンで表した場合の三角関数y = sinx のグラフを描いてみよう。図のようにx軸上に中心をもつ半径1の円を描き,この円周上に点Pをとる。∠ACPの大きさ(符号つきのAPの長さx)を始点Aから測ると,sinxの値は点Pからx軸へ下ろした垂線の長さ(= 点Pのy座標)となる。それをxの関数としてグラフに描くために,点Pをx軸に並行に移動して,原点Oからxの距離まで移動した点をQとし,点Pが円周上を1周以上移動した場合や反時計まわりに移動した場合も含めてすべての場合について,点Qの描く軌跡を記録する。すると,この点Qの描く軌跡がy = sinxのグラフとなる。
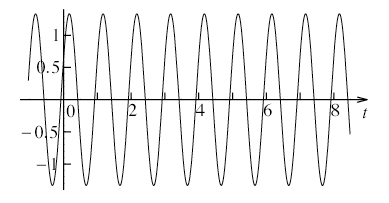
例えば円周を24等分し,0≤x≤2πの範囲でy = sinxのグラフを描くと,下図のようになる。
x < 0あるいは 2π < xの場合には,上図と同様の曲線が繰り返されることが推測できよう。この曲線を正弦曲線あるいはサインカーブという。サインカーブのように周期的に同じ関数値が現れる関数を周期関数という。
周期関数は,一般的には次のように定義される。
|
関数y = f(x)に対してある定数aが存在し,すべてのxについてf(x + a) = f(x)が成立するとき,f(x)は周期関数であるといい,このようなaの最小のものを周期という。 |
明らかに,y = sinxは周期2πの周期関数となっている。
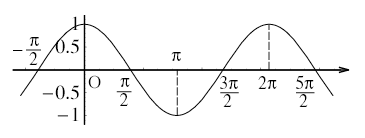
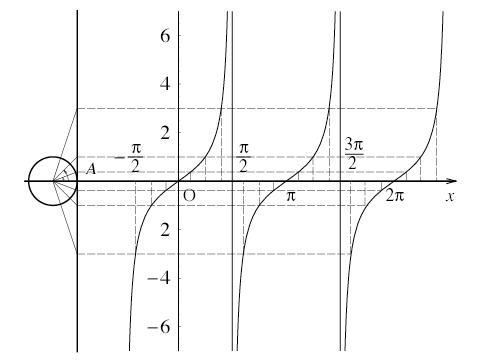
三角関数y = cosxやy = tanxについても同様に考えてグラフを描くことができる。これらのグラフは次のように周期2π,周期πの周期関数となっている。
関数y = cosx
関数y = tanx
以上で三角関数の基本形について述べてきたが,工学の分野で扱う三角関数はy = Esin(ωt+φ)のような形をしていることが多い。この形の関数は,例えば,単振動(バネに重りを吊るし,抵抗のいっさい無い状態で自由に振動させた場合の重りの運動)における時刻tと重りの位置との関係を表す際に現れる。電気的現象においても,交流発電機により発電された電圧や電流の他,随所で現れる非常に重要なものである。
単振動を特徴づける量には,振幅,位相,周期,振動数などがある。ωt = xとして,前述の関数をy = Esinx, y = sin(x + φ), y = sinωtと分解して表し,それらの量について順に説明する。
(1) 振幅(y = Esinx)
y = sinxのグラフは,半径1の円周上を動く点Pから導いたが,ここで半径をEとして考えてみよう。
上のグラフは,y = sinxのグラフが上下にE倍に引き延ばさたものとなっている。すなわちy = Esinxのグラフはy = sinxのグラフを上下にE倍に拡大(Eが1より小さい時には縮小)して得られるもので,単振動であれば重りの運動が運動の中心を原点としてアEの範囲で起こることを表している。このEを振幅という。
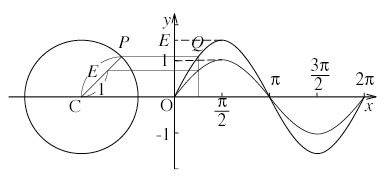
(2) 位相(y = sin(x + φ))
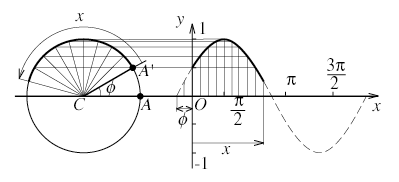
y = sinxのグラフでは,点Pは円とx軸の交点(下図のA点)を始点として回転を始めるように考えたが,ここで始点を円周上の任意の点A'としてみよう。すると,A'からの回転角xを横軸にy = sinxのグラフを描いた時と同様の操作でグラフを描くと,下図のようなグラフが得られる。
CA'とx軸の成す角をφとおくと(∠ACA' = φ),回転の様子から,上のグラフは,y = sinxのグラフよりφだけ進んだ回転の様子を表すグラsフと考えられる。このφを初期位相という。y = sin(x + φ)のグラフは,x = 0の時の値がsinφ(このことが「位相がφだけ進んでいる」の意味である)となる。
(3) 周期と振動数(y = sinωt)
y = sinxのグラフでは,関数の独立変数を角xとしたが,ここでそれを時刻tとしてみよう。すなわち,点Pはt = 0でx = 0の位置にあり,単位時間あたりωラジアン回転するものとする。このωは,回転の速さを表す量で,角速度という。t時間後の回転角はωtであるから,y = sinωtのグラフとy = sinxのグラフは全く同じ形であるが,横軸の数値がt = 2π/ωで表されるものとなり,次のようになる。
この関数の周期は,T = 2π/ωである。また1/Tを振動数という。
以上のことを考慮して,y = Esin(ωt + φ)のグラフを描いてみよう。
下図は,E = 4/3, ω = 2π, f = π/6,すなわち振幅4/3,初期位相π/6,周期1,振動数1のグラフである。
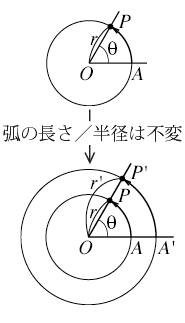 これに対して,左図のように半径rの円において点Pが点Aを始点として回転しているとき,Pの移動した距離APを半径rで割った値AP/rを用いて回転した角度を表す方法がある。この方法を弧度法という。すなわち,θ =∠AOP = AP/rと定義する。この表し方は円の大きさが変わっても,図に示すように円の相似性により不変である。すなわち,図においてAP/r = A'P'/r'より,∠AOP = A'P'/r'と定義してもよい。従って,r = 1とすれば数値的には単純に∠AOP = APである。ただし意味的にはAP/1と考えている。
これに対して,左図のように半径rの円において点Pが点Aを始点として回転しているとき,Pの移動した距離APを半径rで割った値AP/rを用いて回転した角度を表す方法がある。この方法を弧度法という。すなわち,θ =∠AOP = AP/rと定義する。この表し方は円の大きさが変わっても,図に示すように円の相似性により不変である。すなわち,図においてAP/r = A'P'/r'より,∠AOP = A'P'/r'と定義してもよい。従って,r = 1とすれば数値的には単純に∠AOP = APである。ただし意味的にはAP/1と考えている。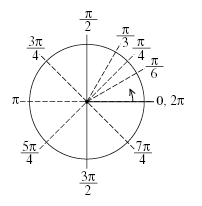
 角を図形的なものとして考える時には角は0から2πまでの値で十分であるが,角を回転量を表すものとして考える時には,何周回転しているか,また時計回りに回転しているのか反時計まわりに回転しているのかといったことによって,2πより大きい角や負の角も考える必要が生じる。その場合,左図のような角が与えられても,その大きさはθ1ともθ2ともθ3ともあるいはその他の角とも考えられ,その表し方に工夫が必要である。ところで,これらの角の値の差はすべて2π(1回転)の整数倍になるので,次のように表すことにより,すべての場合を示すことができる。
角を図形的なものとして考える時には角は0から2πまでの値で十分であるが,角を回転量を表すものとして考える時には,何周回転しているか,また時計回りに回転しているのか反時計まわりに回転しているのかといったことによって,2πより大きい角や負の角も考える必要が生じる。その場合,左図のような角が与えられても,その大きさはθ1ともθ2ともθ3ともあるいはその他の角とも考えられ,その表し方に工夫が必要である。ところで,これらの角の値の差はすべて2π(1回転)の整数倍になるので,次のように表すことにより,すべての場合を示すことができる。
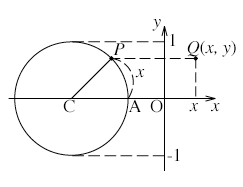 それではここで,角をラジアンで表した場合の三角関数y = sinx のグラフを描いてみよう。図のようにx軸上に中心をもつ半径1の円を描き,この円周上に点Pをとる。∠ACPの大きさ(符号つきのAPの長さx)を始点Aから測ると,sinxの値は点Pからx軸へ下ろした垂線の長さ(= 点Pのy座標)となる。それをxの関数としてグラフに描くために,点Pをx軸に並行に移動して,原点Oからxの距離まで移動した点をQとし,点Pが円周上を1周以上移動した場合や反時計まわりに移動した場合も含めてすべての場合について,点Qの描く軌跡を記録する。すると,この点Qの描く軌跡がy = sinxのグラフとなる。
それではここで,角をラジアンで表した場合の三角関数y = sinx のグラフを描いてみよう。図のようにx軸上に中心をもつ半径1の円を描き,この円周上に点Pをとる。∠ACPの大きさ(符号つきのAPの長さx)を始点Aから測ると,sinxの値は点Pからx軸へ下ろした垂線の長さ(= 点Pのy座標)となる。それをxの関数としてグラフに描くために,点Pをx軸に並行に移動して,原点Oからxの距離まで移動した点をQとし,点Pが円周上を1周以上移動した場合や反時計まわりに移動した場合も含めてすべての場合について,点Qの描く軌跡を記録する。すると,この点Qの描く軌跡がy = sinxのグラフとなる。