2.3 加法定理

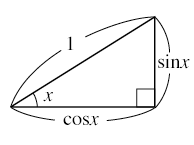
　三角関数の定義より，sin, cos, tanについて次の公式が成り立つことが解る。

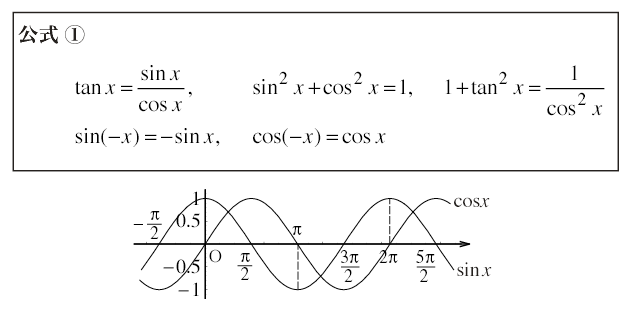
　また定義より，あるいはグラフを見ることにより，cosx = sin(x + π/2)であること，すなわち余弦関数(cos)は正弦関数(sin)の位相がπ/2だけ進んだものであると理解することができる。

　一般に三角関数について，位相がπ/2の整数倍だけずれたとき，次の変形公式が成立する。

　その他三角関数についてはいろいろな公式が成立しているが，その基礎となる最も重要な公式は，次に示す加法定理である。

証明

　まず，0 ≤ α ≤ 2π, 0 ≤ β ≤ 2πの場合について示す。

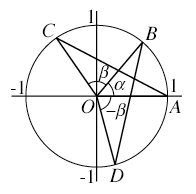　図のように単位円周上に点A, B, C, Dをとる。各点の座標を求めると，A(1, 0), B(cosα, sinα), C(cos(α + β), sin(α + β)), D(cosβ, -sinβ)となる。

△OACと△OBDは合同であるから，AC = BDである。

ここで

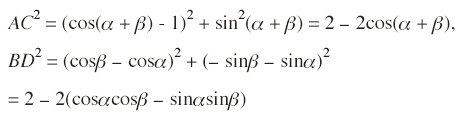
よって

ここで より

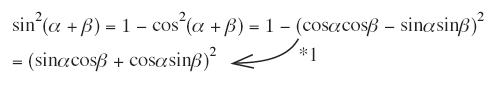
条件より，sin(α + β) ≤ 0, sinαcosβ + cosαsinβ ≤ 0であるから

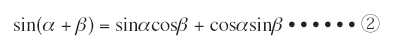
またにおいて，βのかわりにπ/2 - βを代入すると

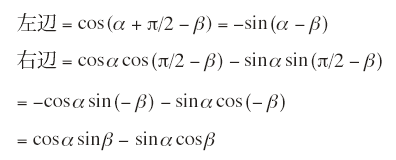
よって

において，βのかわりにπ/2 - βを代入すると，同様の計算で次式がでる。

では次にα, βが一般の角でも定理が成立することを示す。

　θ₁, θ₂ を0以上π/2以下の角として，α = θ₁ + n₁π/2, β = θ₂ + n₂π/2と表しておくと

右辺は，n₁ + n₂がどのタイプの整数かにより，公式の４つの場合に分かれる。

例えば，n₁ = 4m + 2型，n₂ = 4m + 3型とすると，n₁ + n₂ = 4m + 1型となり

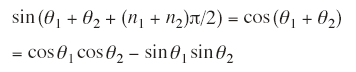
このとき

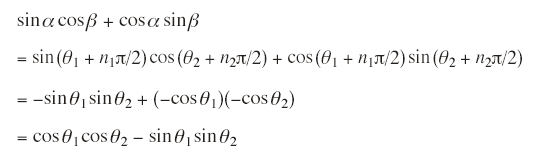
よって

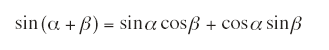
が成立している。

　残りのsin, cosに対する公式も，同様に考えればよい。tanの加法定理については，sin, cosの加法定理を利用して求めることができる。

問１　加法定理の証明において，

(1) *1, *2の部分を計算せよ。

(2) n₁ = 4m + 1型，n₂ = 4m + 2型 とするときcosの加法定理が成立することを確かめよ。

問２　sin, cosの加法定理を使って，tanの加法定理を示せ。

問３　cos(7π/12)の値を求めよ。