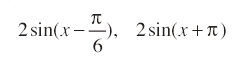前節で学んだ加法定理を変形することにより，その他の公式（2倍角の公式，半角の公式，積を和になおす公式，和を積になおす公式）が得られる。
証明
2倍角の公式については，加法定理
において，α = βとすればよい。
半角の公式については，2倍角の公式より出る。
問１
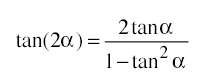
を示せ。
証明
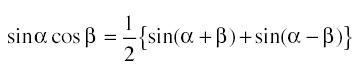
を示す。
加法定理
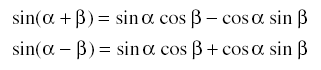
の両辺をそれぞれ加えると
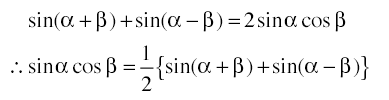
残りの公式は，sinとcosの別の加法定理を組み合わせて両辺を加えるなり，引くなりすれば求まる。
問２ 積を和になおす公式の残り３つを示せ。
証明
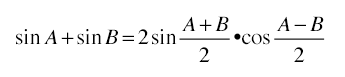
を示す。
積を和になおす公式
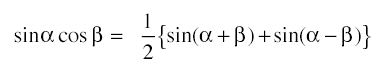
において，α = (A + B)/2, β = (A - B)/2とおくと，A = α + β, B = α - βとなり
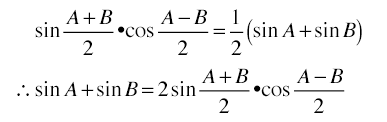
残りの公式は，別の積を和になおす公式において同様の置き換えを行えば求まる。
問３ 和を積になおす公式の残りの３つを示せ。
以上，この節で示した公式は無理に憶える必要はない。必要なときに加法定理から自力で導ければそれに越したことはないが，このような公式があることを知って，必要に応じて使えればよい。
これらの公式以外に，応用上重要なものとして単振動の合成がある。
すなわち，２つの単振動E1sin(ωt + φ1)とE2sin(ωt + φ2)とがあるとき，これを合成して１つの単振動E0sin(ωt + φ0)を求めることである。これを求める準備として，asinθ + bcosθを１つの三角関数で表すことを考えてみよう。
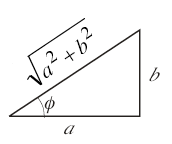
それでは，上の公式
を利用して
が成立するような，振幅E0，初期位相φ0をE1, E2, φ1, φ2を用いて求めてみよう。
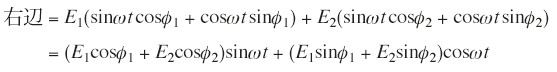
従って最後の式において，
として公式を適用すればよい。すなわち次のようにまとめられる。
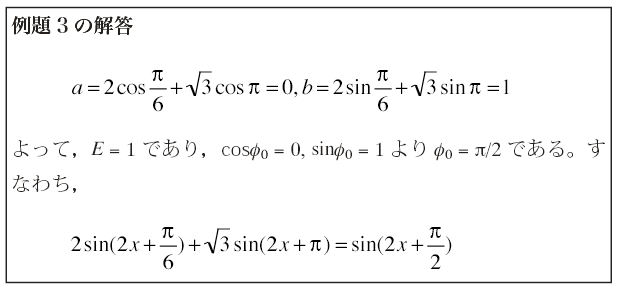
以下に例題3の２つの単振動を合成した結果のグラフを示す。
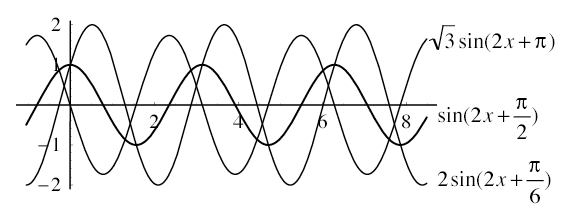
問４ 次の２つの単振動を合成した式を求めよ。
