第３章　複素数

　実用上重要な正弦波交流は，第２章で学んだ三角関数さえしっかりと身に付けておけば，確実に取り扱うことができる。正弦波を表すために必要な量は，振幅，振動数（周期），初期位相といったものであったが，それらは，オイラーの式を媒介にしたフェーザ表示（回転ベクトルの初期状態，複素数で表示）というものでも表すことができる。フェーザ（複素表示）を用いると，定常状態にある交流回路の解析で，三角関数の微分・積分が方程式から無くなり，式の取り扱いが簡単になる。また，電圧や電流の解析を図的に行うことも可能となり，直感的な理解が容易になる。その原理については電気回路理論で学習するが，ここではその基礎となる複素数の取り扱い，波や振動とフェーザとの関連，三角関数「言葉」とフェーザ「言葉」の翻訳などを身に付けることにしよう。

3.1 複素数の直交表示

　数を実数の範囲内に限っていたのでは，２次方程式x² + 1 = 0の解は存在しないことになる。そこで，この方程式の解として，実数ではないが2乗すると-1になる新しい数を考え，それをと書くことにする。このを虚数単位という。虚数単位を用いて，2や1+のような新しい数を作ると，２次方程式x² + 4 = 0やx² + 2x + 2 = 0も解を持つようになる。このように実数と虚数単位の積と和によって作られる新しい数を複素数という。

　すなわち，２つの実数a, bと虚数単位を用いてa + bという形で書かれる数を複素数という。特に，a + 0と書かれる数を実数aと同一視する。また，0 + bと書かれる数を単にbと書き，純虚数という。

　複素数を表示するとき，虚数単位をいつもと書くのはめんどうなので，数学では通常iを用いて表す。電気関係では電流の記号にiを用いることが多いため，虚数単位にはjを用いることが多い。

　2つの複素数の4則演算（和，差，積，商）については，j = なる約束のもとで，jを単なる文字と考えて実数係数の多項式を計算するのと同様に行えばよい。

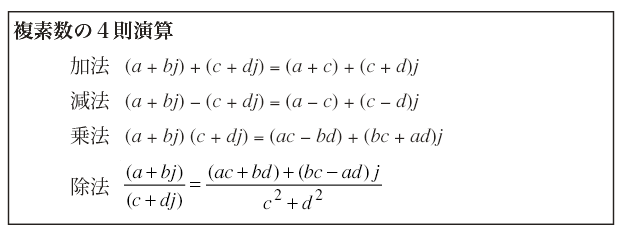
問１　次の計算を行え。

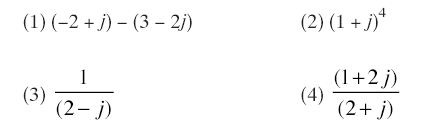
　複素数a + bjを1つの文字で表す場合，よくzが用いられる。z = a + bjとおくとき，aを複素数zの実部といい，Re(z)と書く。また，bを複素数zの虚部といい，Im(z)と書く。虚部をbjと勘違いしないように！ またをzの絶対値といい|z|と書く。

　z = a + bjに対して， = a - bjとおきをzの共役複素数という。明らかに，

が成立している。

　z = 0のときは，a, bともに0となる。

問２　z = 2 - 3jについて，Re(z), Im(z), |z|, zを求めよ。

　実数を下図のように直線上の点として表したものを数直線という。

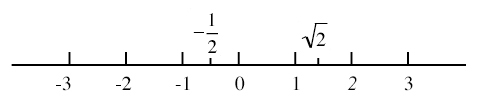
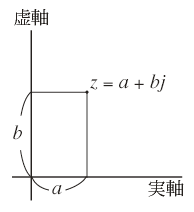
複素数は実部，虚部という２つの実数によって定まる数なので，複素数を幾何学的に表す場合は左図のように平面を用いる。

　複素数の加法と減法を複素平面上の点を用いて理解してみよう。

　z₁ = a₁ + b₁j, z₂ = a₂ + b₂jとすると，

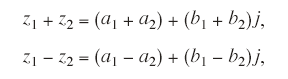
であるが，z₁, z₂の表す点を終点にもつ位置ベクトルOz₁, Oz₂を考えると，ベクトルOz₁ + Oz₂の終点がz₁ + z₂を表す点となっている。またOz₁ - Oz₂の終点がz₁ - z₂を表す点となっている。すなわち，複素数を複素平面上の点として表した場合，複素数の加法と減法はその点の位置ベクトルの加法と減法に対応していることが解る。

　それでは乗法と除法についてはどうであろうか。これについては加法と減法ほど単純ではない。複素数の乗法と除法を幾何学的に理解するには，複素数の表し方を次の§で説明する極表示を用いる方が便利である。

　極表示に対して，この節で述べたように，複素数をa + bjという形で表すことを複素数の直交表示という。