3.2 極表示とフェーザ

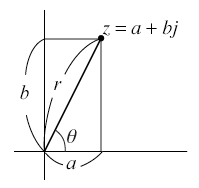
　複素数z = a + bjを左図のように複素平面上に表したとき，線分Ozの長さrがzの絶対値|z|である。線分Ozと実軸の成す角θをzの偏角といい，arg(z)と書く。このとき

である。

よって，

と表される。

　以上のように，複素数を実部，虚部という２つの要素a, bを用いてa + bjと表すかわりに絶対値と偏角という２つの要素r, θを用いてr(cosθ + jsinθ)と表すこともできる。後者の表示法を複素数の極表示（三角関数による）という。

問2　次の複素数について，|z|とarg(z)を求めよ。

　それでは，極表示において複素数の乗法と除法を見てみよう。

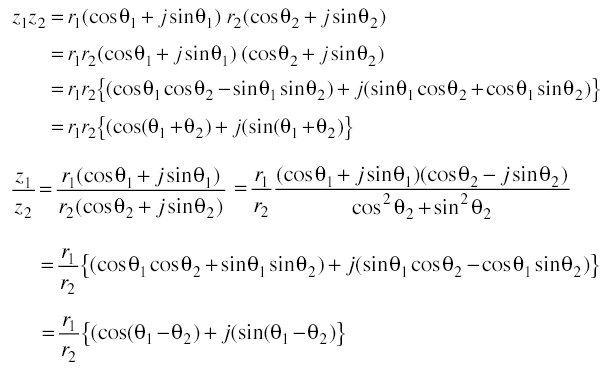
　以上の計算より，２つの複素数の積をとると，絶対値はそれぞれの絶対値の積となり，偏角はそれぞれの偏角の和となることが分かる。すなわち以下の関係が成立している。

　また，2つの複素数の商をとると，絶対値はそれぞれの絶対値の商となり，偏角はそれぞれの偏角の差となる。すなわち

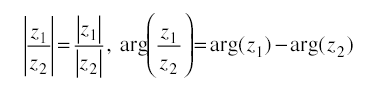
が成立している。

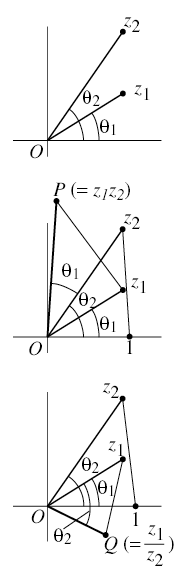　この結果を複素平面上で幾何学的に見てみよう。図のように複素平面上にz₁, z₂を図示する。

(1)積の場合

　実軸上に1の表す点をとり，△O1z₂を作る。△O1z₂と相似な三角形△Oz₁Pを作る。1 : |z₂| = |z₁| : OPよりOP = |z₁||z₂|, OPと実軸の成す角= θ₁ + θ₂。よって，点Pの表す複素数がz₁z₂となる。

(2)商の場合

　実軸上に1の表す点をとり，△O1z₂を作る。△O1z₂と相似な三角形△OQz₁を作る。1 : |z₂| = OQ : |z₁|よりOQ = |z₁|/|z₂|, OQと実軸の成す角= θ₁ - θ₂。よって，点Qの表す複素数がz₁/z₂となる。

　上の計算結果からも明かなことであるが，例題1の結果は，複素数zに虚数単位jを掛けることはzの偏角にπ/2を加えることに，またjで割ることはzの偏角からπ/2を引くことに等しいことを示している。一般に，ある複素数zに複素平面上の単位円周上にある偏角φの複素数を掛けたり割ったりすることは，zの偏角にφを加えたり引いたりすることと同じ結果を及ぼす。

　以上説明してきた複素数の乗法や除法と絶対値や偏角の関係は，更に複素数の表示方法を次に示すオイラーの公式を用いて書き換えれば，指数法則として理解できる。オイラーの公式は複素関数論で学ぶものであるが，ここでは1つの表示方法であると考えておいてよい。

　ここに現れる文字eはネピアの定数といわれるもので，円周率を表すπと同じように循環しない無限小数で，e = 2.7182818...である。しかし，ここでは単に記号としての文字と思っておけばよい。

　オイラーの公式を用いると，絶対値がr，偏角がθである複素数zは

と表すことができる。この表示方法も極表示（指数関数による）という。

　極表示（指数関数による）における乗法と除法は次のようになる。

とおくとき，

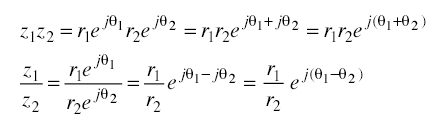
　上の等式は，極表示において，jやθなどを単に指数の文字と思って通常の指数法則を使って計算してよいことを示している。

問3　次の複素数を直交表示は極表示に，極表示は直交表示になおせ。

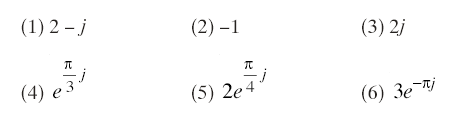
　複素数の表示法をまとめておこう。

　電気関係においては，大きさと位相という2つの量によって定まるものをフェーザと呼び，複素数を使って表示する。

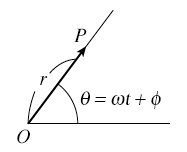　左図のように，Oを基点とする1本の基準線と，Oを中心に回転する動径上の向きのついた線分OPを考える。以後この線分を動径OPという。動径OPは大きさrと位相θの2つの量によって定まる。

　位相θは，初期位相φと角速度ωにより決定されるが，一定角速度で回転することを考慮して，一般に位相としては初期位相を与える。このように考えた動径OPをフェーザといい，複素平面に描いたものをフェーザ図と呼ぶ。

　複素数は，絶対値と偏角によって定まるので，フェーザ（動径OP）の大きさに絶対値を，位相に偏角を対応させて，フェーザを次のように複素数を用いて

と表すことにする。

であるならば，時には

と表すこともある。またこのテキストでは簡単のためにフェーザを単にアルファベットの大文字で表すこともある。

　このように動径OPを用いてフェーザという概念を導入するのは，多くの電気的現象の中には，動径を仲立ちにすることにより理解が鮮明になる場合が数多く存在するからである。例えば交流電流や電圧などがフェーザとして把握される例であるが，これらの応用面については次の3.3節で詳しく解説することとし，ここでは第2章で学んだ単振動を例に上げて説明しよう。

　2.2節で学んだように，単振動Esin(ωt + φ)は下図のような大きさE，初期位相φ角速度ωの動径OPによって導かれる。

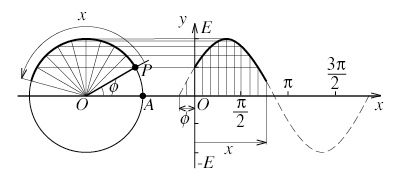
このことをおさえて，2.4節の例題2-3をフェーザを使って解いてみよう。

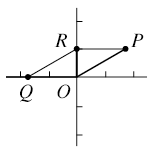　単振動2sin(2t + π/6) - - とsin(2t + π) - - をフェーザとして捉える。すなわち，は大きさ2，初期位相π/6の動径OP，は大きさ，初期位相πの動径OQと考える。動径OP，動径OQの和は，ベクトル演算より動径ORとなる。従って単振動と単振動の合成は動径ORの表す単振動である。これを複素数表示して計算すると

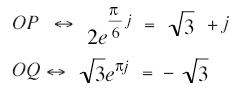
よって

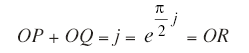
　すなわち，この2つの単振動の合成はと複素数表示されるフェーザにより導かれるものである。すなわち，sin(2t + π/2)となる。

　以上の結果をまとめると次のようになる。

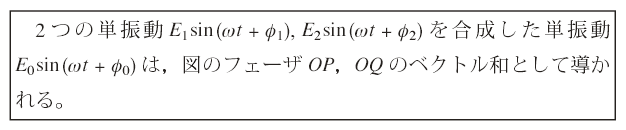
　2つの単振動を合成する場合，ここで示したようにOPとOQのベクトル演算により得られるフェーザORとして求めてもよいし，E₀, φ₀の具体的数値を2.4節の公式により求めてもよい。ただし，ここで注意しなくてはいけないことは，単振動Esin(ωt + φ)をフェーザとして捉え，

と表したときに，右辺は左辺のあくまでも1つの表示であると理解しておくことである。すなわち，「机」は日本語で，「desk」は英語であるように，同じ対象物を表現できるが言葉としては別言語であることに似ている。これを等しい（=）と勘違いするとおかしなことになる。また，電気回路ではフェーザの大きさとして，単振動の振幅の分の1を用いるという実用的な約束もあるので注意が必要である。